"EcoSSe - Eco Spatial Statistical evaluation", Envirosoft 2000, Bilbao, Spain, June.

EcoSSe -- Eco Spatial Statistical evaluation

Isobel Clark

Geostokos (EcoSSe) Limited, Scotland.

Abstract

EcoSSe is a new Windows NT and 95/98 based application which has been developed from the more elaborate mining package, Geostokos Toolkit. It provides facilities for basic statistical analysis and advanced geostatistical analysis of sample data located in two dimensions.

The Toolkit software has been developed over 25 years with some of its main extensions prompted by environmental work. For example, simulation methods were developed during work on the proposed nuclear waste isolation project in Texas in the 1980’s (ONWI), whilst methods to deal with highly skewed distributions were prompted by investigation of toxic waste leakages into groundwater in Eastern USA. EcoSSe has been produced to provide the non-specialist user with a "cheap and cheerful" approach to geostatistical analysis. Documentation includes tutorial runs to familiarise the user with the features and use of the package in both statistical and geostatistical routines. All documentation is written using a minimum of jargon and practical data sets for illustration.

This software is available now but expected to develop considerably over year 2000 as the needs of users become apparent. Unlike many other software companies, we expect our users and colleagues to suggest new applications and features at any time. We are also striving to make the software "user transparent" so that the user can concentrate on the analyses he/she wishes to carry out and not on how the software works.

1 Introduction

One of the major problems associated with environmental assessment, potential pollution problems and other types of earth science applications is that of producing maps from severely limited sample information. For example, in groundwater pollution studies, samples may only be available from existing water wells or limited extra drilling. The well sites will not have been selected to best reflect quality of the groundwater and will usually be sub-optimal for assessing pollution risk levels. Normal mapping packages may are unlikely to give adequate representation of the variables under study for several reasons:

· Most standard mapping methods assume a smooth continuous phenomenon, like a topographic surface;

· Mapping packages use only local variability ignoring large scale trends or dispersion patterns;

· Interpolation methods tend to work best with well-behaved Normal sample data;

· Gridding methods work best with sample data which is fairly evenly distributed across the study area -- not clustered or highly irregular spacing.

To illustrate these problems we present two case studies. The first is from the ONWI studies carried out in the mid 1980’s [1] and shows the effect of clustered data and a strong trend in values on subsequent maps. The second data set is taken from a paper on dioxin contaminated residues dumped on a road in Missouri [2] and illustrates a skewed distribution.

2 Wolfcamp Case Study

As part of the risk assessment study for a proposed high level nuclear waste repository in north-west Texas, detailed investigations were carried out into the aquifers underlying the site. One of these aquifers, the Wolfcamp, is used by local ranchers for water wells. Measurements on 85 wells were available after eliminating over- and under-pressured wells. The measurement of interest in our current illustration is the pressure of water in the aquifer, expressed as potentiometric level in ‘feet above sea level’. As can be seen from the post plot in Figure 1, pressure tends to be higher in the south-west and drops off significantly towards the north-east. The Figure also shows that the water wells tend to be highly clustered.

Figure 1: post plot of Wolfcamp sample information

Geostatistical interpolation (like many other methods) is based on an assumption of no strong trend in the sample values. In cases where trend exists, the values are assumed to be composed of two components: a deterministic trend surface plus a ‘stochastic’ or statistical variable. Any interpolation method must include both components to be realistic. Trends can be fitted to the data:

Figure 2: quadratic trend surface fitted to Wolfcamp data

It can be seen that individual sample values will differ from the ‘trend’ value at any specified location. These differences -- or residuals -- should be “detrended” and ordinary interpolation methods should be applicable. To map using geostatistical methods, we produce a weighting function known as the semi-variogram which models the continuity or predictability of values from one location to another.

Figure 3: semi-variograms from original Wolfcamp data showing strong trend

Figure 4: semi-variograms after quadratic trend has been removed

Notice in particular the difference in scale between the semi-variogram graphs before and after removing the trend component. Over 92% of the variation in the original data is accounted for by the trend in values. The other 18% can be interpolated by any mapping method. The geostatistical method known as “Universal Kriging’ will estimate the value at any given location and account for the trend as well as the continuity modelled in the semi-variogram.

One of the major advantages of a geostatistical approach to mapping is that every grid point estimated has an error associated with it. The likely size of this error is described by the ‘kriging standard error’ and is generally interpreted as the standard deviation of the estimation error. The logical consequence of this is that a kriging estimation produces two maps -- one for the estimation and one of standard errors.

The map of standard errors can be used to indicate where estimates are less reliable -- and, hence, where more sampling may be needed. The standard errors can also be used to produce simulations to test the sensitivity of the resulting maps. For example, the kriged map produced the ‘best’ estimate of values at given locations. However, the ‘true’ surface will be considerably rougher (more variable) than indicated by these smooth contours. Simulation puts back the roughness and allows us study likely variations between this ‘best’ answer and equi-probable outcomes. We used simulations to study the travel paths for radio-nucleides in the event of breech of the repository [3].

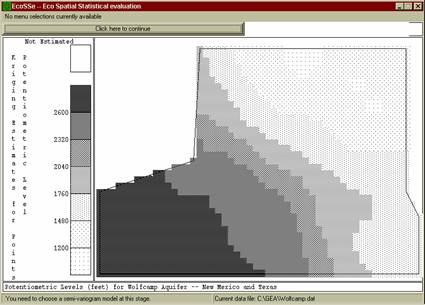
Figure 5: estimated map for potentiometric level in Wolfcamp aquifer

Figure 6: standard errors for prediction of potentiometric levels in Wolfcamp

The kriging interpolation technique is optimal in the sense that it minimises the estimation variance subject to the semi-variogram function and the locations of the samples used in the estimation. There are several implications which may not be immediately apparent:

· Kriging is an exact interpolator, honouring the sample data at the data locations;

· Kriging compensates for clustering in data locations, allocating weights to each sample which are adjusted by the inter-sample relationships as well as by the sample--estimated point relationship;

· Universal kriging automatically compensates for trend.

3 Missouri dioxin pollution

A truck transporting dioxin contaminated residues dumped an unknown quantity of these wastes onto a farm Road in Missouri. In November, 1983, the U.S. EPA collected samples of the site. In order to reduce the number of samples required, samples were composited along transects. The transects run parallel to the highway, and this direction is designated as the X-direction. The direction perpendicular to the highway is designated as the Y-direction. Data are TCDD concentration (tetrachlorodibenzo-p-dioxin) in micro grams per kilogram (mu g/kg).

This data set is complicated by two factors:

1. A large proportion (55 of 127) of the sample data is given a flat value of 0.1 mu g/kg. This phenomenon usually occurs because the values of the samples fall below some "detection limit" and an arbitrary low value is assigned to the samples. The probability plot in Figure 7 shows these ‘non detects’ clearly.

2. Those measurements which have been taken follow a highly skewed distribution with a coefficient of variation of around 16.

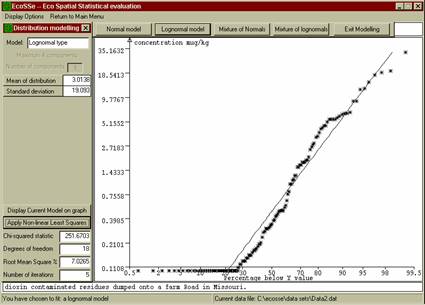
Figure 7: probability plot of dioxin measurements along contaminated road.

Problem (1) above may be tackled by using an ‘indicator’ approach to discriminate between ‘non detect’ and ‘detect’ samples. In an indicator transform, all non detects would be replaced by the value ‘0’ and all detects (measured sample values) by ‘1’. A semi-variogram graph is constructed from these zero and one values, showing whether we can predict the likely occurrence of detectable values at any specified location. Figure 8 shows the semi-variogram obtained using an indicator value of 0.25 mg/kg.

Eliminating the non detect samples from consideration leaves us with a data set which is extremely highly skewed. Mapping these values with no allowance for this skewness will produce erroneous estimates. In general, high values will be smeared out of all proportion to their true influence and low values underplayed. Whilst the high values are of most interest to us in pollution studies, a realistic estimate is more desirable than one which is unduly alarmist.

Several alternatives are available to us for dealing with highly skewed data. In many cases a simple logarithmic transformation results in Normally distributed values -- that is, the original measured values follow a lognormal distribution. Figure 9 shows that this is quite likely for this set of sample data.

Figure 8: indicator semi-variogram for detect/non-detect in dioxins

Figure 9: probability plot of dioxin values grouped to eliminate tail

If a suitable parametric model cannot be found, rank transforms can be applied. Figure 10 shows a semi-variogram calculated from this data set using a rank transformation in value. The difference between the behaviour of measured values and ‘non detects’ can be clearly seen in this graph.

A similar graph was produced using a logarithmic transformation for measured sample values.

Summary

We have endeavoured to illustrate some ways in which a geostatistical analysis will differ from mapping by more conventional packages. This type of approach allows for methods which reflect the true distribution of the sample data -- both spatially and statistically.

A geostatistical analysis can also form the basis for risk assessment in pollution and other environmental studies, allowing for quantitative measures of confidence and reliability to be attached to such studies.

All illustrations in this paper have been produced using the EcoSSe package. Additional information on the EcoSSe software can be found at http://www.kriging.com or from ecosse@kriging.com.

Figure 10: semi-variograms on rank transform of dioxin value showing detect/non-detect problem.

References

[1] Harper, W.V. & Furr, J.M. Geostatistical analysis of potentiometric data in the Wolfcamp Aquifer of the Palo Duro Basin, Texas. Technical Report BMI/ONWI-587, Battelle Memorial Institute, Columbus, OH. 1986.

[2] Zirschy, J.H. & Harris, D.J. Geostatistical analysis of hazardous waste site data. Journal of Environmental Engineering, Vol:112, pp. 770-784. 1986.

[3] Harper W.V. & Clark I. Travel Path Uncertainty -- Two Approaches to Conditional Simulation. Proc. 4th Int. Conf. on Solving Ground Water Problems with Models, February, pp.149--162, 1989.