Poster Session Only
The Mine Call Factor --- conditional bias at its worst
Isobel Clark
Geostokos (Ecosse) Limited
Alloa Business Centre
Whins Road, Alloa FK10 3SA
e-mail: isobel@kriging.com
William V. Harper,
Department of Mathematical Sciences
One
614-823-1417 Fax:
614-823-3201
e-mail: WHarper@otterbein.edu
Abstract
This poster presentation will illustrate the problems of declining Mine
Call Factors (MCFs) particularly in the Wits gold
mines. The significant increase in “gold losses” in many mines over the last
few years can often be explained by updating the
“regression corrections” first introduced by krige in the 1950s.
The regression effect (or conditional bias) is a well
known problem and is encountered, to some extent, in all producing
mines. theoretical methods of correction are
available. This poster session will demonstrate the relative merits of:
(a) classical
regression corrections
(b) simple
volume/variance calculations
(c) stope-by-stope
conditional bias correction
One of the effects which is generally not
appreciated is that skewed distributions have a different kind of conditional
bias from that in Normal distributions. The volume/variance effect in Normal
distributions is clear cut and generally well
understood: cutoffs below the mean value over-estimate grade and under-estimate
tonnage; cutoffs above the mean over-estimate grade and over-estimate tonnage.
With the lognormal distribution, the crossover on tonnage is a lot less clear cut since the distribution of the logarithms changes
in median as well as in variance. Compare the grade/tonnage
curves for logarithms (based on
Introduction
In South African gold mines, the major measure of the efficiency of the
production process is the “Mine Call Factor” (MCF). This factor compares the
gold estimated in situ by the
surveyors (or geologists) with the amount of gold finally produced by the plant
--- with allowance for losses to tailings. The factor is
generally expressed as the ratio between the “gold called for” and the
gold accounted for, as a percentage.
In recent years, many mines have been experiencing declining MCFs and numerous investigations have
been undertaken to try to establish the causes on a mine by mine basis.
There are many potential ‘physical’ causes for the loss of gold in a producing
mine, ranging from gold blasted into backfill bags up to gold theft syndicates
which seem to operate successfully on many mines. However, recent studies (cf.
de Jager, 1996) indicate that the popular mythology
of gold lost in cracks and washed into gullies cannot begin to explain the
recent plunges in the MCF in major mines.
The purpose of this presentation is to review the more traditional
sources of apparent gold loss --- that is, in the initial valuation of the gold
in place in the stopes. In this poster
we illustrate the difference between what is expected from stope valuation and what is actually from a stope panel. This exposition is
based on a set of real sample data from a
The
Case Study
For the purposes of this study, we have taken an area approximately
2000 metres square within a producing mine. This area has
been mined continuously in recent years and is still in production. To
avoid major complications, we have chosen a reef which
is lognormal but not too highly skewed. This is not a very high
grade area, but neither is it marginal at current costs. The reef under
study is also a moderately thick reef, since extra complications arise in the
sampling and valuation of very narrow reefs. In short, we have chosen an area which should be well behaved as regards variations in
value.
This area has been sampled on the usual basis of face samples every
five to six metres, taken at regular intervals as the stope advances. As in
most traditional mines, the sample information follows a very rough ‘grid’ of
about five to six metres in the two-dimensional plane of the reef. Sampling was carried out by hand chipping channels across the reef.
The individual sections of the reef are combined to
provide a single average value across the reef at the sampled location.
It is usual to estimate the value in the stope by averaging the values
in the stope face. In some cases, more than one face is used
to estimate the remainder of a stope. For this study, we have simplified the
situation as follows:
·
a face is taken to be a 100 metre stretch of
samples, usually 5 or 6 altogether;
·
a planning block
is taken to be a 100 by 100 metre rectangular stope panel.
Obviously, the study as described here can be carried
out for other geometries and stope sizes.
The estimated gold values as produced by the survey office consist of
the average value for all samples on the face, divided by the stoping width
planned for that stope. We have emulated the ‘true’ stope panel values by
simply averaging all of the sample values within 100 by 100 metre panels across
the study area. This is the closest we can expect to come to the actual
resource figures. In this particular study area, we have just under 2000 panels
with sufficient sampling to serve our purposes.
Grade/tonnage
curves
To compare the estimates produced from the face sampling with the
‘actual’ values in the stopes we have constructed
“grade/tonnage” curves --- more commonly known on the gold mines as
“payability” graphs. In brief, we apply a cutoff value or pay limit to the values and calculate the percentage of the area which is expected to be above this cutoff and the
average of the values over this ‘payable’ percentage. This exercise was carried out on:
(a)
the individual channel samples;
(b)
the 100 metre face averages;
(c)
the 100 by 100 metre
stope panels.
The theoretical grade/tonnage graph shows the comparison between the
percentage payabilities for the three different
‘support’ sizes: point, face average and area average. It can
clearly be seen that there is a significant difference between the
percentage payability in the three cases.
Of more concern, perhaps, are the results shown in the lognormal
grade/tonnage curves. This graph shows the average value of the payable
proportion of the area. It is quite obvious from this
graph that, the bigger the area selected, the lower the achieved grade for a
specific cutoff or pay limit. The two graphs taken together show that, for a
larger volume of ground, the average grade will always be lower than for a
smaller area. This is a direct consequence of averaging over a volume or area.
A payable area on average may well
contain unpay material which will be mined. On the
other hand, unpay stopes
may well contain payable material which will be left behind.
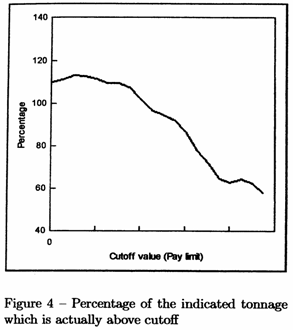
It can also be seen that --- for high cutoffs
--- the tonnage in payable stopes is considerably
less than that indicated by the face sampling.
Mine
Call Factor
The Mine Call Factor (MCF) is generally expressed as the “gold called
for” versus the “gold accounted for”. However, this is
expressed in different ways by different mines. In many cases, the ratio
calculated is between the average grade in grams of
gold per tonne of ore estimated versus grams per tonne of ore milled. That is,
the MCF would be the grade found in the stope divided by the grade measured on
the face expressed as a percentage. If we perform this calculation on the lower
two lines in the grade/tonnage graph, we can obtain an illustration for how the
MCF would change with rising pay limit in our case study area.
There seems to be little cause for concern in this case study, since
the MCF varies between 89 and 99 per cent depending on the pay limit. That is,
in general, the stope value will be approximately 91% of that value predicted
by the face sampling. Most mines work with this level of MCF without concern.
However, it is necessary to look also at the graph to determine what tonnage is being considered here. There is a crossover point at
which the tonnages in face and stope become equal. At cutoffs below this point,
there is more tonnage available in stope panels than indicated by the faces.
For cutoffs above this point, the reverse is true with considerably less
payable tonnage available in stopes than might be
expected. It is clear that the ratio of grade called for to grade achieved is
only really valid at the point where the comparison
between tonnages is 100%. This graph is analogous to the factor often known as
“surveyor’s shortfall”.
Alternate
scenarios
From the above analyses it can be seen that many stopes
which appear to be payable according to the face sampling will go ‘unpay’ at some point. There are two possible scenarios which can be considered here:
·
what happens when we select whether or not to mine
the panel on the basis of the face value;
·
selecting whether or not
to mine on the ‘true’ average value over the panel.
For a particular production situation these
two scenarios could be studied in detail. For the purposes of this study, we
interpreted the two alternatives as follows:
·
compare grade obtained from payable stopes with that obtained from faces which were payable at
the same pay limit;
·
compare the gold recovered
against the gold expected according to the predictions.
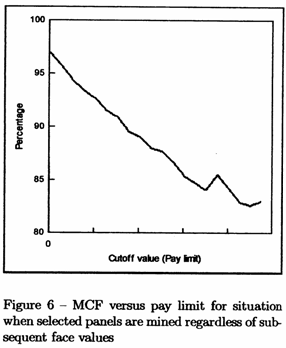
These two scenarios are shown as two graphs.
Comparing the face value against the actual panel value mined, the grade call
for this moderately skewed case is pretty stable until
half way through the range. However the gold recovered
is significantly below that predicted --- and the comparison becomes extremely
unstable for high cutoffs. If we take the panels which
were actually payable, we see that the grade call is pretty stable at around
90% of expected value. The gold recovered is higher than expected
for the first half of the graph and then drops drastically as the cutoff rises
into the tail of the distribution.
Conclusions
It has been said that there are many possible
physical causes for the apparent loss of gold indicated by a falling Mine Call
Factor. In this paper we have not considered these
factors although they can contribute significantly to a low MCF. Neither have
we considered such problems as the accuracy of the sampling process underground
and the assaying process in the laboratories. What we have attempted to show in
this paper is that significant declines in the Mine Call Factor may well be due
to the valuation process itself and to the management decisions
which are based on those valuations.
In previous years, when the pay limit or cutoff values stayed at a
consistent level --- below the ‘crossover point’ --- Mine Call Factors remained
reasonably consistent over long periods, albeit with considerable fluctuations
on a month to month basis. With rising costs in the mines and rising pay
limits, the actual decision process to mine or not to mine a stope becomes of
increasing importance in the maintenance of a reasonable Mine Call Factor and,
thus, of an efficient producing gold mine.
Reference
de Jager, E.J. (1996)
“the analysis of the Mine Call Factor in gold mining, with specific reference
to Western Holdings Mine”, PhD thesis, University of the