I

I. Clark, C.T.P. Williams and S.N. Smithies, "TRIPOD - a computer program for evaluating borehole sampling in gold projects", J. Inst. Min. Surv. S. Afr., Vol 23, pp.109- 116

TRIPOD - A COMPUTER PROGRAM FOR EVALUATING

BOREHOLE SAMPLING IN GOLD PROJECTS

by Dr. C.T. P. Williams, Gencor Geostatistics Department,

Dr. Isobel Clark, Geostokos Ltd.,

Mr. S.N. Smithies (Member), Gencor Geostatistics Department

1. SYNOPSIS

This paper describes the use and operation of a computer program called TRIPOD which replaces the use of graphs and tables for the evaluation of gold deposits from drilling results. A sample session using fictional but typical sample values is shown. The program runs on the IBM Personal Computer, but may be used on other computers.

2. INTRODUCTION

The estimation of potential gold ore reserves for prospective mines in Witwatersrand Conglomerate reefs is a crucial and well established process. Generally the information on which the estimate must be based consists of geological observations and assay values from diamond drilling intersections. Within the structural and sedimentological constraints imposed by the local geology, an estimate of mineable reserves must be made from a few very costly sample points which are frequently separated by many hundreds of metres.

After the selection of samples which are to be included in the estimation process has been made, the procedure is automatic: there are no decisions which need to be made up to the point at which an estimate of the in-situ value is completed. Thereafter, to arrive at an estimate of mineable reserves, many other considerations enter the process.

The accepted approach to the valuation problem in these conditions of widely spaced samples is to regard the borehole values, usually the arithmetic mean of the width-grade accumulations from acceptable deflections, as independent observations from a single population. The distribution is usually modelled with a three parameter lognormal model with the parameters estimated from observations of the log-probability graph.

An estimate of the mean value of the population and confidence limits for this estimate are found by using the model parameters and Sichel's (1966) t-tables, or Wainstein's tables. Linear interpolation is used between the values provided on the existing tables.

A stoping variance is then assumed or derived and the well-known graph GRL20 is used to read off the payability and pay value for selected pay limits.

These graphical and tabular methods have been necessary in. the past because of the considerable calculation involved in arriving at some of the required figures and therefore the impracticability of doing these computations separately for each estimate. The arrival of cheap and rapid computing facilities in recent years has changed the situation to the extent that this process can now be computerised.

3. TRIPOD

In March 1986 Gencor Geostatistics Department commissioned GEOSTOKOS Ltd., of London to provide computer subroutines, written in the FORTRAN 77 programming language, to enable these calculations to be done by computer without the need to refer to tables or read values from graphs. The programs were installed at Gencor Head Office in Johannesburg in July 1986, and two weeks later at Winkelhaak Mines Ltd., on the Evander goldfield where they were tested in practical applications. The subroutines were written in FORTRAN to enable them to be compiled and used on most microcomputers, although the IBM PC-AT was the computer currently in use at Gencor.

The author of the FORTRAN code of the subroutines (I. Clark) will be publishing the details of the mathematical and statistical processes used in TRIPOD. The aim of this paper is to explain what the program does and its practical applications. The subroutines have been written to follow accurately the existing logic used in the accepted valuation methods, so that, for example, Sichel's tables or graph GRL20 can be reproduced by TRIPOD. There are however some points on which it may be possible to make some improvement to the existing logic and these will be discussed in the later publication.

TRIPOD is the name given by Gencor Geostatistics Department to the overall program which successively uses several specialised subroutines to carry out each part of the evaluation process. The sequence of operation is summarised as follows.

4. DATA ENTRY

The program needs a computer file containing the individual borehole values. Various ways of entering this information can be through prompts on a terminal screen for each value by a subroutine built into the TRIPOD main program or by using an editor program, or with a sophisticated database applications program. After initial testing at Winkelhaak Mines Ltd., it became clear that the latter method would be the most satisfactory and a user friendly "menu" selection and entry "screens" were subsequently added to TRIPOD.

The interactive session described later in this paper does not include the initial entry of the borehole values. The file used, called DIANE.DAT, contains the co-ordinates, channel width, lithology type and various other pieces of information in addition to the cmg/t values. These extra observations need not necessarily be used in TRIPOD but may be used to select sub-areas or lithological types if desired; they are also very valuable if other types of analysis are to be carried out on the borehole results, such as semivariogram analyses or machine contouring.

The values in DIANE.DAT are from a fictional prospect called DIANE, but are quite similar to the type of information on which gold prospects must be evaluated.

5. FITTING THE 3-PARAMETER LOGNORMAL MODEL

After reading the date file, TRIPOD calls a subroutine to find acceptable values for the three parameter lognormal model. The user has the option of choosing a two parameter model if desired.

Two alternative methods of fitting a model to the observed results are given and statistics are provided for the "goodness-of-fit" of the model. If needed, the program can be modified very simply to enable the user to over-ride the fitted third parameter model. When the user is satisfied with the model the program proceeds to the next stage.

6. SICHEL'S T ESTIMATE

The method outlined by Sichel and used to construct the well-used tables, is utilised to provide an estimate of the mean of the lognormally distributed population. This phase of the program is very fast, taking about one second of time.

The user is then requested to provide up to ten confidence levels (percentage probabilities above which the mean value is estimated to lie), likely choices being 10% and 90% confidence limits. This stage of the program requires considerable computational resources and an IBM PC-AT may take as long as two minutes for four confidence levels to be calculated.

When the mean value and confidence limits have been found the program proceeds to the next stage.

7. PAYABILITY AND PAY VALUE (GRL20)

At this stage the user is given the option of specifying a "block variance", the variance of the logs of the block mean values, or calculating it. The borehole model variance which for DIANE is about 0,6, is displayed. If the user decides to calculate the block variance, the program will prompt for a semivariogram model and a block geometry. However if the semivariogram is not known, the user may wish to specify a block variance, and 0,2 appears to be a popular arbitrary choice.

The program then requests a number of pay limits to be entered. Up to twenty may be chosen, although for most purposes ten may be adequate. In the sample session shown here, the user specified ten pay limits from 500 to 950 cmg/t. The total in-situ tonnage before selection is also requested.

The payability, the percentage of the blocks which will have mean values lying above the pay limit, and the pay value, which is the mean value of the ore, are displayed as a table, together with the tonnage of ore. The user may respond to requests to obtain the three forms of grade tonnage curves for the deposit, over the range of pay limits chosen.

8. FUTURE DEVELOPMENT OF THE PROGRAM

The program has been structured so as to be quite general in its application and thus refers to in-situ reserves only. For the evaluation of prospective gold mines, decisions must be made as to the likely milling width, metallurgical recovery, mine call factor and the quantity of unpayable ground which must be mined to gain access to the ore. A further subroutine, coded DILUTE, is under development in Gencor Geostatistics Department which will enable the user to interactively specify these factors, and observe the effects on the prospect valuation.

The output from TRIPOD shown here has been directed to simple printers and screens which operating mines are likely to have attached to their microcomputers. More sophisticated plotter routines may also be used to provide more accurate and stylish graphs of the log-probability plots and grade-tonnage curves.

9. EXAMPLE SESSION

Table 1 shows a listing of the borehole information file (DIANE.DAT) with the standard format used in TRIPOD and many other programs in the library of geostatistical subroutines.

Annexure A shows the text which appears on the screen of an IBM PC-AT during an evaluation session. The results which appear on the screen are also written into a computer file during the session so that when the estimation is complete the user can request a printout of the results.

A session such as this occupies a user, with one days' experience, for about a quarter of an hour. The entry of the borehole values prior to the session may take about an additional half hour. This time ' is very much less than would be needed by an experienced person using graphs and tables, and the opportunities for errors are less.

10. AVAILABILITY

The software used in TRIPOD is currently available under a multi-use licence to all the operating mines of the Gencor Group. However the proprietary copyright to the major subroutines resides with Geostokos of London.

REFERENCES

Krige, D.G. (1962) Statisitical Applications in Mine Valuation, J. Inst. Mine Survey S. Afr. 12(2), 45-84, 12(3), 95-136.

Krige, D.G. (1981) Lognormal-de Wijsian Geostatistics for Ore Evaluation, S. Afr. Inst. Min. Metall Monograph Series, Johannesburg, 2nd Edition.

Rendu, J.M. (1981) An Introduction to Geostatistical Methods of Mineral Evaluation, S. Afr. Inst. Min. Metall. Monograph Series, Johannesburg.

Sichel, H.S. (1966). The estimation of means and associated confidence limits for small samples from lognormal populations. Symposium on Mathematical Statistics and Computer Applications in Ore Evaluation, 106-122. S. Afr. Inst. Min. Metall, Johannesburg.

Storrar, C.D. (1981) South African Mine Valuation, Chamber of Mines of South Africa, Johannesburg.

Wainstein, B.M. (1975). An extension of lognormal theory and its application to risk analysis models for new mining ventures. J. S. Afr. Inst. Min. Metall, 75, 221-238.

TABLE 1

A LISTING OF BOREHOLE FILE DIANE.DAT

DIANE GOLD MINES 42 Boreholes SICHEL'S ANALYSIS

42 8 0

Borehole Number Block Number Type Number Y Co-ordinate

X Co-ordinate Channel Width cmg/t No. of deflections

1636 1 1 19244.5 12272.8 28.6 519.8 4

214 1 1 19000.8 11946.2 19.1 240.0 3

191 1 1 19176.3 11687.5 16.7 1744.8 2

213 1 1 19425.6 11724.8 16.8 288.5 3

211 1 1 19627.2 11418.0 22.0 1216.2 3

917 1 1 19313.7 10892.4 26.8 2098.0 3

883 1 1 19494.6 10323.2 28.8 1258.5 4

216 1 1 19945.0 9802.5 19.1 1023.5 3

1635 1 1 19592.8 10039.5 48.6 268.6 2

1632 1 1 19944.2 10385.8 61.7 366.9 6

196 2 1 20125.2 10405.2 20.4 199.0 2

831 2 1 20285.4 8955.2 59.8 588.2 2

850 2 1 20067.0 9309.4 35.2 189.0 3

918 2 1 20588.4 10647.4 26.8 2098.0 4

938 0 1 19849.0 11150.1 26.5 32.3 4

782 4 1 20960.0 7975.0 17.4 1637.8 3

683 4 1 21349.6 7789.0 25.1 389.2 3

687 4 1 20895.0 7661.2 63.1 741.2 2

442 4 1 21149.6 7254.0 17.0 2425.0 3

684 4 1 21150.2 6642.2 19.9 830.7 3

961 4 1 21496.9 6347.4 46.3 749.9 4

438 2 1 20477.3 8370.8 39.9 264.9 2

463 3 1 21983.2 7053.2 21.5 584.5 3

469 2 1 20823.8 9396.5 18.5 386.8 3

727 3 1 22186.1 6154.6 18.4 284.8 3

929 2 1 21333.8 9239.8 24.4 87.1 9

949 2 1 20703.0 8948.7 49.4 266.1 4

1580 1 1 19305.0 11228.4 36.8 350.7 5

1562 1 1 19643.7 10736.1 25.1 348.2 4

1458 1 1 19056.3 10472.1 23.1 497.4 6

1623 1 1 19862.8 10291.6 24.6 2556.8 8

1606 1 1 19659.3 9596.5 51.8 2019.6 4

1459 1 1 19258.0 9613.9 60.8 1258.5 4

1630 1 1 20326.8 10813.4 29.6 57.2 4

1498 4 1 20720.5 6883.7 89.6 946.4 4

1609 4 1 21025.4 6922.0 23.6 795.9 4

1627 4 1 21490.2 6975.3 86.5 687.7 4

1499 4 1 21242.2 6013.0 23.8 90.8 4

1603 4 1 21953.9 5882.4 26.0 652.9 4

1634 4 1 21509.7 5410.5 85.0 353.2 4

458 4 1 21829.6 5472.8 21.5 1252.3 3

1518 3 1 21510.7 5065.0 25.5 327.1 6

ANNEXURE A

An example of an interactive session with TRIPOD using the DIANE.DAT borehole data.

C: \GEA> TRIPOD - AN INTERACTIVE PROGRAM FOR EVALUATING LOGNORMAL SAMPLING

Welcome to the Geostokos Software:

designed to perform Statistical and Geostatistical analysis of sample data from mining projects

There are various options open to you, as regards output:

1. a minimum of output only to terminal screen

2. lots of output to the screen

3. some information on the terminal screen, most of it written onto a file for later printing

4. lots of output to the terminal screen, plus copy written onto a file.

Please state your choice - -> 4

Your output will be written onto a file called STOKOS.PRT

is this acceptable? yes

Name of input data file, please - -> diane.dat

Does this file have Borehole ID's? no

What values indicate a missing measurement?

anything less than - -> 0

Do you want a full listing of all the data? No

The title for this data is:

DIANE GOLD MINES. 42 Boreholes. SICHEL'S ANALYSIS

There are 42 samples on this file with 8 observations on each.

Index	Variable
1	Borehole Number
2	Block Number
3	Type Number
4	Y Co-ordinate
5	X Co-ordinate
6	Channel Width
7	cmg/t
8	No. of deflections

Please specify variable of interest by number, for example: 2 would mean "Block Number"

Your choice? 7

Do you want me to take logarithms of the values? No

Which area do you want to analyse?

(type 0 for all areas) - -> 0

DIANE GOLD MINES. 42 Boreholes. SICHEL'S ANALYSIS

There are 42 samples in this data set with 8 observations measured on each.

Please wait, reading in data.

Finished reading in data file

Do you want to use a THREE PARAMETER lognormal? Yes

There are 42 "cmg/t" values

Starting to calculate percentage points:

4.99999 Point no. 1 Level 5.00%

9.99989 Point no. 2 Level 10.00%

9.99981 Point no. 3 Level 90.00%

4.99989 Point no. 4 Level 95.00%

Percentage Confidence

No. Confidence Level

1 5.00 1147.19

2 10.00 1061.73

3 90.00 673.91

4 95.00 637.60

The samples have a logarithmic variance of .8328

In the "payability" calculations, do you want to:

(a) Use this variance

(b) change to a "block" variance - -> b

Do you want to specify the block variance? Yes

What is the block variance? .2

How many pay limits do you want? 10

Please specify pay limit value:

1 --> 500

2 --> 550

3 --> 600

4 --> 650

5 --> 700

6 --> 750

7 --> 800

8 --> 850

9 --> 900

10 --> 950

What is the total tonnage before selection 40000000

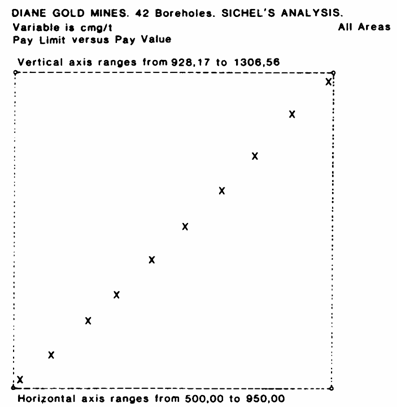
Pay Limit Pay Value Payability Tonnage

500.00 928.17 79.53 31810250.

550.00 962.02 73.36 29345220.

600.00 998.88 66.98 26793260.

650.00 1038.21 60.61 24243200.

700.00 1079.58 54.41 21765230.

750.00 1122.63 48.53 19410390.

800.00 1167.06 43.03 17212280.

850.00 1212.65 37.98 15190060.

900.00 1259.20 33.38 13351590.

950.00 1306.56 29.24 11696350.