
Software Tutorial --- lognormal statistics
The example session with PG2000 which is described below is intended as an example run to familiarise the user with the package. This documented example takes you through the following sequence of analyses:
{#} Reading in a data file
{#} Summary statistics and scatterplots of the data
{#} Scatterplot of the data using transforms
{#} Fitting a log-normal distribution to the data
{#} Re-estimating the average of the distribution and relevant confidence levels
There are many other facilities within the package, which are given as alternative options on the menus. To start the tutorial, choose PG2000 from your Start menu. When you run PG2000, a record is kept of everything you do in that run. The default name for this file is ghost.lis and the default location for the file is the folder where your copy of PG2000 is kept. The first dialog you will see is:

You may change the name of the file, or accept the default. In some operating systems, the file extension may not be shown in the window or the File name box. The default file name is ghost.lis.
You may change the name of the file, or accept the default. Note you must type in the whole name including extension, since no default extension is offered in this case. For example, if you want to call your ghost file "myghost.lis" you need to type the whole name, not just "myghost".
If you already have a file with this name, Windows will issue a warning:

Click on ![]() to specify a new name or
to specify a new name or
![]() to overwrite previous copy of this file.
to overwrite previous copy of this file.
Your screen should now show something like:
![]()
The output above is the opening screen. To proceed to data analysis, use one of the menus at the top of the Window.
Reading in a data file

As you can see from the above I have elected to read in a
set of sample data by clicking on the ![]() option and selecting
option and selecting ![]() from the menu which appears. PG2000
will remember the last five data files accessed and include these in your
options.
from the menu which appears. PG2000
will remember the last five data files accessed and include these in your
options.
I have selected GASA.DAT for my input data file. This is a set of 27 boreholes taken from a lease area at project (pre-feasibility) stage in the life of a typical Witwatersrand gold mine. The sample data are real values disguised by a factor. The boreholes are averages of several deflections --- ranging from 1 to 8 on each hole --- and are roughly a kilometre apart.

Even if you select a file from the list of previously analysed data files, PG2000 will ask you to confirm your choice. This is actually a quick way of getting back to your working directory, since you can change your choice at this point. Be warned, though, that if you change which file you want to read it must be the same type of file – that is, if you are reading a standard Geostokos data file, you cannot change your mind at this point and read in a CSV type file.

For this example, we will stick with GASA. As your data is read in, it is stored on a working binary file. A progress bar will indicate how far the process has gone. When data input is complete, your Window should look like the table above.
The routine which has been used shows the first 10 lines of your data file so that you can check it is going in OK.
The routine also checks whether we actually had the correct number of samples on the file and informs you if there is any discrepancy. Notice the "number of samples" message. In the GASA file, someone typed '72' instead of '27' in the header line. The software checks the number of samples and informs you if it doesn't match with the header line.
![]()
Scattergram or scatterplot
When the data has been read in you will see that the
previously "greyed out" or inaccessible options on the main window
toolbar will become activated. You can now select an option. Let us decide upon
a statistical analysis. To do this, click on the
![]() option on the main toolbar.
option on the main toolbar.

If you choose the ![]() option, you will display and summarize the
data set and will enable you to get an idea of what the data set looks like in
a simpler form than the full numerical listing.
option, you will display and summarize the
data set and will enable you to get an idea of what the data set looks like in
a simpler form than the full numerical listing.
The screen will switch to a dialog which will prompt you to choose the two variables for the axes of your graph.
The active screen in the top left hand corner contains the variables available for analysis in your data file. The bottom right box shows the variables already chosen (which at this point is none).

This screen provides you with a lot of information. The bottom of the Window contains a "status bar" which shows the name of the current data file and the title read from that file. Above this "status bar" is a box containing the title of your data set as read from the first line of your input data file.

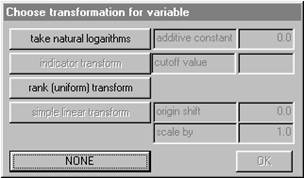
The ![]() dialog box shows you that you are expected to
select variables to be the X co-ordinate and the Y co-ordinate for your
scattergram. The upper left dialog box
dialog box shows you that you are expected to
select variables to be the X co-ordinate and the Y co-ordinate for your
scattergram. The upper left dialog box
![]() lists the variable names as they appeared in
the data file, and is prompting you to choose the variable which will be the X
co-ordinate on the graph. For this example, let us choose Easting for the X
co-ordinate. You need to check the box next to the Easting option.
lists the variable names as they appeared in
the data file, and is prompting you to choose the variable which will be the X
co-ordinate on the graph. For this example, let us choose Easting for the X
co-ordinate. You need to check the box next to the Easting option.
Upon selecting the Easting option, a new dialog box will
appear asking you whether you wish to transform the variables to logarithms or
rank transforms. In this case we do not wish to transform so we click on
![]() . The dialog disappears and you
will be asked for the Y co-ordinate:
. The dialog disappears and you
will be asked for the Y co-ordinate:

I selected the Northing option by clicking its check box.
The transformation dialog again appeared, from which choose not to transform
the variable by clicking on
![]() .
.
The lower dialog moves up to the top left and displays your
current working variables. The
![]() and
and ![]() buttons have now been activated. If you change
your mind at this point, simply click on the
buttons have now been activated. If you change
your mind at this point, simply click on the
![]() button and you will be returned to the
original dialogs.
button and you will be returned to the
original dialogs.
Clicking ![]() will show you your scattergram. The
scattergram is scaled to fit the whole of the display box or area.
will show you your scattergram. The
scattergram is scaled to fit the whole of the display box or area.

Please note that even though you have chosen 'geographical' variables, the scale chosen is for the maximum display size. If you want points plotted on a 'geographical' scale (same for both axes) you must use the post-plotting routine which is available elsewhere in PG2000.
In the left-hand box of the graphical display, you will see the summary statistics for both variables plus the product moment correlation coefficient and the number of samples for which both variables were available.
When the graph is completed, you can select a new option
from the main toolbar. You may wish to plot another graph in which case you
must click on ![]() and select the
and select the ![]() option again.
option again.
Scattergram 2, using transformations
To illustrate the use of the transformations for the
variables, we draw another graph showing the logarithm of the gold grade. Upon
selecting the ![]() option
your screen should show:
option
your screen should show:

PG2000 will remember your previous selection.
Since you are redefining your variables, you must click on ![]() to redefine your variables. You will again be
asked to select the X co-ordinate and the Y co-ordinate. For the first variable
we simply take logarithms. For the second we add a constant to the variable so
that the transformation actually becomes Normal (Gaussian) - the determination
of such a constant is described later in this demonstration run.
to redefine your variables. You will again be
asked to select the X co-ordinate and the Y co-ordinate. For the first variable
we simply take logarithms. For the second we add a constant to the variable so
that the transformation actually becomes Normal (Gaussian) - the determination
of such a constant is described later in this demonstration run.
For the X co-ordinate check the corresponding box of the Width of reef (cms) option

and then select the take natural logarithms option in the new pop up Window. Because you chose the logarithmic transform, you are prompted for an additive constant. If such a constant is not required - as for Width of reef (cms) simply type 0 (zero) or leave the default unchanged.
Make sure you click on ![]() to confirm your requested transformation.
Until you do so you can still cancel the transformation by clicking on the
to confirm your requested transformation.
Until you do so you can still cancel the transformation by clicking on the
![]() button.
button.
For the Y co-ordinate we want to plot gold grades with an additive constant of 0.230. Thus, check the corresponding Grade (g/t) option, and then select the take natural logarithms option in the new pop up Window. In the required box, type 0.23 as the additive constant value. Your screen should look something like the picture on the next page.

Make sure you click on ![]() to confirm your requested transformation.
Until you do so you can still cancel the transformation by clicking on the
to confirm your requested transformation.
Until you do so you can still cancel the transformation by clicking on the
![]() button.
button.
Once both variables have been selected, you can change them or accept them as before:
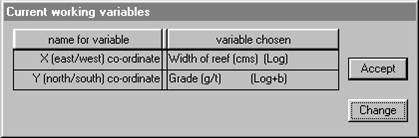
Click on ![]() to plot the final graph (see next page).
to plot the final graph (see next page).

Fitting a three parameter lognormal distribution
Click on ![]() and move mouse pointer down to
and move mouse pointer down to ![]() before letting go of the mouse button:
before letting go of the mouse button:

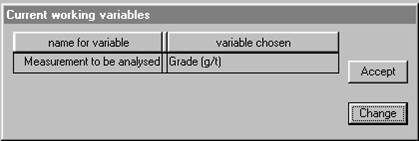
If you have already done some analysis in a run, PG2000 remembers which variables you were analysing. If not, it prompts you to specify which variable is to be studied. Since we have not yet specified a "measurement to be analysed" the following dialogs will appear. We want to analyse gold grade.


Select Grade (g/t) as the measurement by clicking in the
check box, then press the ![]() button.
button.
In this example we have less than 500 samples, so that the distribution may be fitted to all of the original (individual) sample values. If we had more than 500 samples we would have to build a histogram first.


For this example, I clicked on: The large square dialog disappears, leaving
us with the summary statistics and a graph. The probability plot of the data is
constructed and the "best fit" lognormal distribution shown as a
dotted or dashed straight line. That is, the data values will be plotted on the
'Y' (vertical) axis on a logarithmic scale. The percentage of the samples which
fall below a given value is given along the horizontal (X) scale. If the
logarithmic values follow a Normal (Gaussian) distribution then the samples
should give a more-or-less straight line on the plot. The dashed line shows the
perfect Normal distribution with the same mean and standard deviation as the
data.
The large square dialog disappears, leaving
us with the summary statistics and a graph. The probability plot of the data is
constructed and the "best fit" lognormal distribution shown as a
dotted or dashed straight line. That is, the data values will be plotted on the
'Y' (vertical) axis on a logarithmic scale. The percentage of the samples which
fall below a given value is given along the horizontal (X) scale. If the
logarithmic values follow a Normal (Gaussian) distribution then the samples
should give a more-or-less straight line on the plot. The dashed line shows the
perfect Normal distribution with the same mean and standard deviation as the
data.

If the logarithm of the values is Normal, we say that the values themselves are "lognormal". The gold grade values in this data set do not follow a simple lognormal distribution. The lowest value sample lies way below the perfect line. If we use standard lognormal calculations on this data, we will over-estimate the average value of gold in this deposit. Sichel and Krige in the 1950's discovered that such data could be transformed to Normal by adding a constant value before taking logarithms. This 'additive constant' is sometimes referred to as a "third parameter" and the resulting distribution is known as the "three parameter lognormal".
PG2000 will find the additive constant which
most nearly straightens out the line, if requested to do so. Click on the
![]() bar. If the line was already pretty straight
or the curve flattened rather than dropping, a three parameter fit would be
inappropriate. In such a case click on
bar. If the line was already pretty straight
or the curve flattened rather than dropping, a three parameter fit would be
inappropriate. In such a case click on
![]() to return to the main menus. The software will
try many different additive constants to determine the one which produces the
'straightest' line. When this process is finished, it will again display the
probability plot and the straight line which represents the three parameter
lognormal. The parameters of the distribution are displayed in the left hand
(information/option) box.>
to return to the main menus. The software will
try many different additive constants to determine the one which produces the
'straightest' line. When this process is finished, it will again display the
probability plot and the straight line which represents the three parameter
lognormal. The parameters of the distribution are displayed in the left hand
(information/option) box.>

The "Mean value" listed above is the graphical estimate for the mean of the distribution from which the samples were taken. In plainer terms, an estimate of the average grade in grams per ton of the sampled area. Similarly, the logarithmic variance is a graphical estimate --- this time of the variance of the logarithms of the sample values plus the additive constant. The Additive Constant is also given. Skewness and kurtosis have been calculated for the new fit. In an ideal logarithmic Normal, skewness would be zero and kurtosis 3.
In addition to these basic parameters, the "Residual Mean Square" has been listed. This value of 3.96 may be thought of as a typical percentage difference between the sample values and the final lognormal distribution model. This is an intuitive "goodness of fit" statistic which may be used in conjunction with graphical methods of model fitting such as that carried out by this routine. If a histogram had been built, you would also have seen a chi-squared goodness of fit statistic which could be compared to standard statistical tables. You may note that the software tried 52 additive constants before choosing this one.
Best estimate for lognormal mean
We used the three parameter lognormal option to find out whether a three parameter lognormal model was appropriate for our data. During that analysis, we produced the additive constant which best fitted the data. We also produced graphical estimates for the average grade and the logarithmic variance. These estimates gave us a pleasing straight line fit on a sheet of probability paper. However, they are not the "best" estimates for these quantities. Once we have chosen the third parameter --- the additive constant --- we can use Sichel's classical maximum likelihood methods to produce the "best" estimate of the average grade of the distribution. Even better, we can ask for confidence limits on this estimate to get an idea of just how reliable it might be.

The software remembers the variables we are analysing and suggests:
Clicking on the ![]() button results in the following dialog:
button results in the following dialog:

Note that the additive constant box is highlighted so that you can change from the default value if you wish. You may specify up to twenty levels of confidence for the estimate by entering percentages into the first column in the grid. Scroll down if you have too many to be shown all at once.

The choices above will provide lower 95% and 90% confidence
levels plus the upper 90% and 95% levels. If we desired (say) a central 90%
interval, we would use the 5% and 95% levels. Pressing the
![]() button will allow the software to carry out
the calculation of Sichel's t estimator and any requested confidence levels:
button will allow the software to carry out
the calculation of Sichel's t estimator and any requested confidence levels:

You do not need to confine yourself to the traditional levels of risk. Note the 2.735% level for a lower 97.265% confidence limit.
All relevant information on the existing sample set is
present on the dialog. This means that you can copy the dialog with
![]() +
+
![]() and paste it into another application. Some systems (notably Windows NT)
require pressing
and paste it into another application. Some systems (notably Windows NT)
require pressing ![]() +
+
![]() .
The text information is also copied to the GHOST.LIS file.
.
The text information is also copied to the GHOST.LIS file.
Clicking on the ![]() button will pass you back to the main menu. To
finish this run of the program, select:
button will pass you back to the main menu. To
finish this run of the program, select:

Clicking on this menu item or on
![]() will end your run with the software. You will
see the closing down dialog box:
will end your run with the software. You will
see the closing down dialog box:

The above Tutorial session should serve only to illustrate a possible use of the various routines from PG2000. Try running the program again, choosing your own responses. try looking at reef width instead of grade. This variable has a standard two parameter lognormal distribution. Try reading in one of the other data files which are provided, say, samples.dat.
General Notes
There are a few points which you may have noted in following the Tutorial session above. Most of the routines communicate between themselves, without you having to worry about getting the right information from one to the other. For example, after you read in the complete contents of the data file, the routines ask which of the variables you actually want to analysis. This information is then stored internally and may be accessed by any of the other routines. When we went from plotting graphs of one variable against another to fitting a lognormal distribution, the routines knew that you had selected some variables, but that these were inappropriate for the new analysis. On the other hand, going from fitting the lognormal to recalculating the average using Sichel's methods, the routine suggested that you could continue to use the same choice of variables. This is a feature of most of PG2000, in that it will recall what you chose previously and ask whether this is to change or not.
PG2000 does not distinguish between upper and lower case letters, so you may type in whatever you find most pleasing. When the program requires a numerical answer, your input will be checked to make sure that it is actually a number. If you type in any illegal characters and press, the checking routine will filter out the unacceptable characters which you type. It should be noted that, if the routine is expecting a whole number then a decimal point is unacceptable. Much of the numerical input is checked for valid values.
A copy of this run should have been made on a file called GHOST.LIS unless you changed the name at the beginning of the run. Send this file to your printer if you want a record of the analysis or look at it with Wordpad or Notepad.
PG2000 — like any computer software — is not completely error-free. Neither is it fool-proof. You can always get out of the software by right clicking on the Taskbar. This will invoke the 'End Task' facility to close the Window without damaging the rest of your system. If you cannot figure out what went wrong, note down as much information as you can about the program you were running, the data you were using and exactly where it broke down. Contact your supplier locally or Geostokos direct for assistance, software@kriging.com. Send us the ghost.lis file and (if you can) the data you were analysing at the time.
Back to list of tutorials and other good stuff